制御対象のモデリング(作図法)
制御対象のモデリングは、賢い制御系設計をするための基本的な第一歩です。一方で、モデリングまでの道のりや作業内容は非常に泥臭く、制御系設計のウエイトの半分を占める地道なものでもあります。だからこそ、経験と勘で調整できてしまうPID制御も、モデルひとつで理屈ある設計・調整ができるようになります。今回は、以前の「一次遅れ+むだ時間系モデルのステップ応答シミュレーション」に関するエントリの最後でペンディングとなっていたシステムパラメータを求める方法≒制御対象のモデリングについて解説します。方法自体には様々なやり方がありますが、第一弾として、鉛筆と定規だけでできる作図法を取り扱います。
キーワード:モデリング、作図法、ステップ応答
はじめに
モデリングの第一弾を解説するに当たって作図法を紹介する。作図法によるモデリングの技巧的な内容には、
- 鉛筆と定規があれば簡単にできる
- 中央制御室のトレンドからだけでもおおよその読み取りができる
といった点がある。一方で、
- 人や状況次第で、読み取ったシステムパラメータの結果にばらつきが発生しやすい(誤差が大きく精度に欠けがち)
- 正確なシステムパラメータを読み取る上で、ステップ応答波形そのものやそのデータを得るための実験に求める条件が厳しく、モデリングの手法の中でも限定的な方法である
などの欠点もある。
作図法によるモデリング
作図法は、測定した制御対象のステップ応答をグラフ化し、図示によりモデルやシステムパラメータを読み取る・割り出す方法である。ここでは、手順のみを示すに当たり、以下の通りとする。
- プロセス制御でよく用いられる「一次遅れ+むだ時間系」のモデルについての作図法を示す。
- 二次遅れ系や積分系は作図の方法が異なるのもあるが、もっと数値的な解析手法でやった方がよいので、今回は割愛する。
- ステップ応答を測定し終えたものとし、測定のための実験方法自体は別エントリに持ち越す。
- 外乱は気にならないぐらい小さい状況 or 気にならなくなるぐらい大きなステップ応答を測定したと想定してほしい。(フィルタを使った、は状況が変わってくるので×)
<手順>
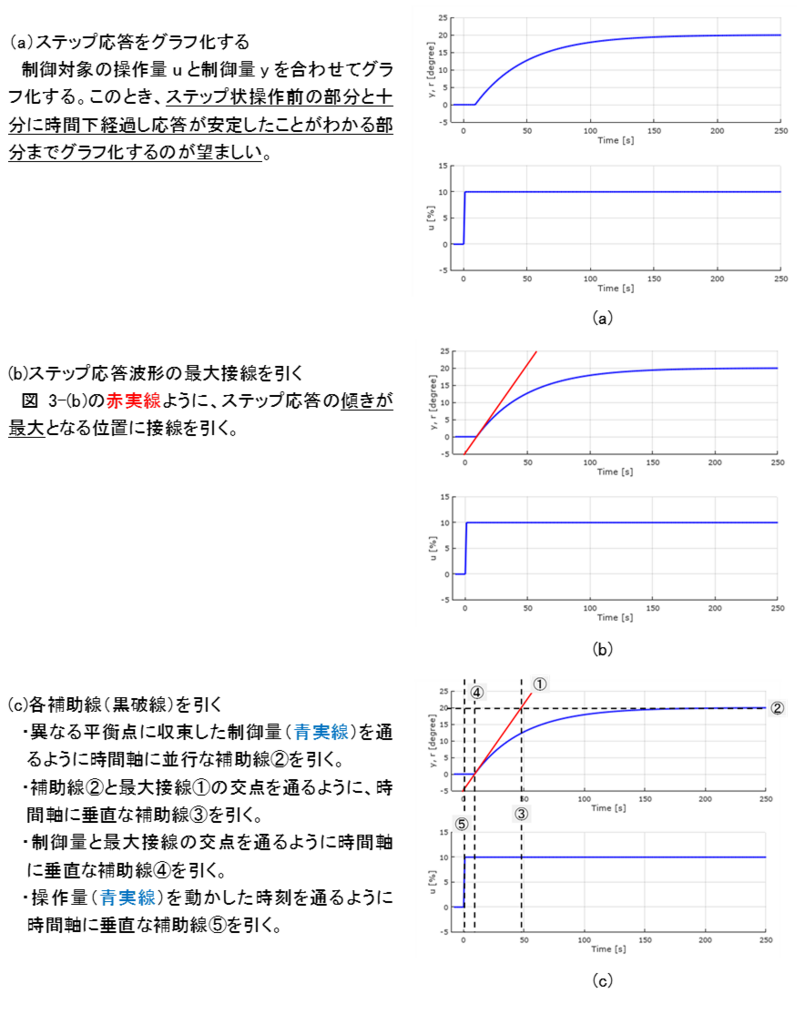
ここまでがグラフに対する作図となる。続いて、システムパラメータを読み取る。
<読み取り方>
- システムゲイン\(K\)(degree/%)
ステップ応答前後の操作量\(u(t)\)と制御量\(y(t)\)をそれぞれ読み取り、いわゆる変化率を計算する。
\begin{align*} K &= \frac{y(\infty) - y(0)}{u(\infty) - u(0)}\\ &=\frac{20 - 0}{10 - 0} = 2 \left({\rm degree} / \%\right) \end{align*} - 時定数\(T\) (s)
制御量が初めて応答する補助線④から③までの経過時間を読み取る。
\begin{align*} T &= 48 - 8\\ &= 40\left({\rm s}\right) \end{align*} - むだ時間\(L\) (s)
操作量を動かした時刻⑤から制御量が初めて応答する④までの経過時間を読み取る。
\begin{align*} L &= 8 - 0\\ &= 8\left({\rm s}\right) \end{align*}
以上が、ステップ応答の作図法によるモデリングである。これでZN法やCHR法、制御シミュレーションを通してPIDパラメータが決定・調整できるようになる。さらにここで、読み取ったシステムパラメータによるモデルのシミュレーションと実際の測定値を比較し、結果が妥当だったか評価するとよい。
作図法に関する補足
<モデルの選択>
今回、制御対象を表すモデルを「一次遅れ+むだ時間系」と仮定したが、本来は、図3-(a)のグラフ化の時点で、制御対象の設備・製造プロセスに関する特性を踏まえ制御量を観察し、
- 減衰振動がない(=二次遅れ系でない)
- 異なる平衡点に収束している(=積分系でない)
- S字曲線のような変曲点がない(高次遅れでない)
- 操作量を動かした後に制御量が応答するまでタイムラグがある(=むだ時間系である)
などから適切なモデルの形を選択することになる。
<時定数\(T\)について>
システムパラメータのうち\(K\)や\(L\)はその定義から、補助線を引かずとも目測で割り出せるが、\(T\)は一工夫が必要となる。どうして最大接線のようなものからわかるのか、その原理を知りつつ、もっと簡略的な読み取り方を補足として解説する。
図示による読み取り手順をそのまま関数で実行してみる。やりまず、一次遅れ系モデルの伝達関数を時間領域の表現にするために、逆ラプラス変換するところから始める。
\begin{align} y(t) &= \mathcal{L}\left [\frac{K}{1+Ts}e^{-Ls}U(s)\right ] \notag \\ &= K\left(1 - e^{-\frac{1}{T}(t-L)}\right)u(t-L) \label{eq:eq20180311-1} \end{align}
これが図3-(a)の制御量(青実線:y(t))となる。また、\(u(t-L)=u_s\neq 0\)(\(t\gt L\))であることを考慮し、(\ref{eq:eq20180311-1})式の変化率の最大値\( \lim_{t \to L}\frac{dy(t)}{dt} = \frac{K}{T}u_s \)から、最大接線は
\begin{align} y(t)=\frac{K}{T}u_s\left(t - L\right) \label{eq:eq20180311-2} \end{align}
となる。したがって、(\ref{eq:eq20180311-2})式と補助線②(\(y(t)=Ku_s\))の交点を通るように時間軸に垂直な補助線③を引くということは
\begin{align} Ku_s &= \frac{K}{T}u_s\left(t - L\right) \notag \\ t&= T+L \label{eq:eq20180311-3} \end{align}
を求めることと同値になり、\(L\)に相当する部分を差し引くことで時定数が求まるのである。
それでは、時定数の簡略的な求め方についても解説を加える。これまでの計算過程で、最大接線が\(T\left(+L\right)\)を求めるために関係が深いことがわかった。\(t=T+L\)のとき、\(y\left(T+L\right)\)の値はどうなるだろうか。結果は(\ref{eq:eq20180311-5})式となる。
\begin{align} y(T+L) &= K\left(1-e^{-1}\right)u_s \notag \\ &=0.632Ku_s = {\rm const}.\label{eq:eq20180311-5} \end{align}
つまり、\(Ku_s\)の約63.2(%)になることがわかり、図3の例だと0.632 * K * us = 0.632 * 2 * 10 = 12.64(degree)となる。したがって、逆算式で考えると、\(Ku_s=y(\infty)\)の約63.2(%)である0.632 * 20 = 12.64(degree)に到達する時刻\(t=48\)を読み取ることで、\(L=8\)を差し引けば\(T=40\)が求まることになるのだ。
小まとめ
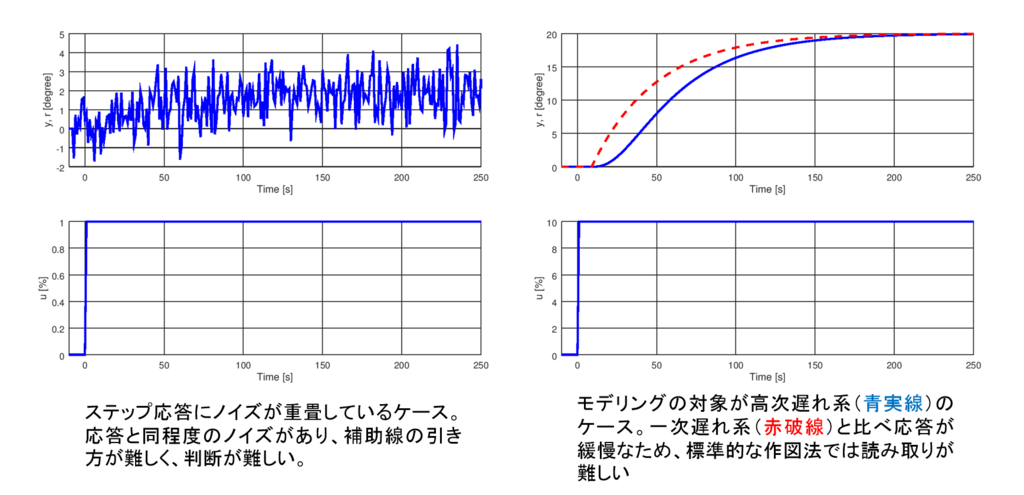
今回、モデリング手法の中で比較的簡単に行える作図法を解説した。実際に遭遇する問題を通してわかることだが、簡単な方法ゆえに応用が利きにくい。様々な設備特性・製造プロセスの中で、ステップ応答による作図法を試みようとすると、この方法では難しい場面に直面する(末尾に添付した図はのその一例)。しかし、作図法の技巧的な部分は、現場でのモデルの概算に役立つ。簡単で応用が利きにくい方法であっても、モデルの一部の特性をつかむだけで、その後の制御パラメータの調整や既存制御の問題点を解明する際に天と地ほどの差ができる。最後に、第二弾では最小二乗法を使ったモデリングについて解説したいと思う。