微分動作の問題点と不完全微分
時間遅れしかないプロセスにとって、未来を予測し位相を進めてくれる微分動作は良心である。単にノイズに弱いからと言って、微分時間を小さく設定したり、PI制御しか使わないのはもったいないです。今回は、PID制御をより実践的に使うための要素技術の一つである不完全微分について解説します。
キーワード:PID制御、微分動作、不完全微分
はじめに
PID制御における微分動作は、温度制御のような応答が遅いプロセスの改善に役立つ。一方で、流量や圧力関係の制御では、ポンプや弁の動作に起因した脈動や乱流で制御量が振動的になってしまうことから、微分動作がそれを増幅し、過大な操作量で制御系を不安定にしたりする。そればかりか、過大なアクチュエータの動作は設備の劣化にもつながる。他にも良くない影響として、非常に大きくなった操作量が有効な操作範囲を超えたり、パルス状になった操作量ではアクチュエータがそもそも動作できなかったりと、本来の制御性能が機能しなくなることもある。これらはすべて、微分動作が振動的あるいは不連続な制御偏差の変化量を使うからである。以下の図1は、微分動作が良くない働きをする例である。
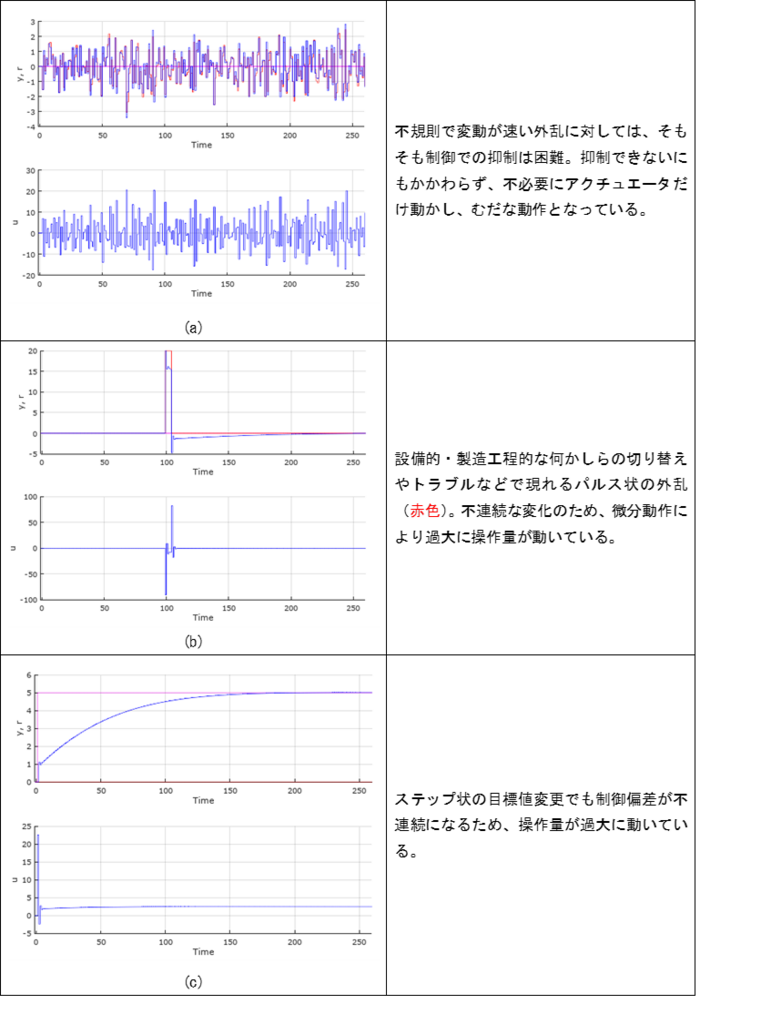
図1:微分動作が良くない働きをする例
不完全微分とその仕組み
振動的あるは不連続な制御偏差\(e\)を単に微分すれば、その変化量は当然大きな値となる。そこで、ノイズのような悪さをする信号だけ取り除く or 制御すべき信号であっても逆に悪さをしない程度の形に緩和すれば、微分動作を使えるようになるはずである。この機能を具体的に実現するには、微分動作\(T_ds\)に図2のブロック線図のような工夫を施す。
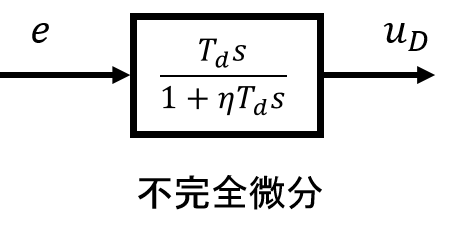
図2:不完全微分のブロック線図
この工夫がどのようなものであり、機能を実現する仕組みは何であるかを考えるために、ブロック線図を分解し、制御偏差\(e\)にインパルス信号を印可・各信号を観察する。詳細は図3の通りで、
- ブロック線図の伝達関数は、「ローパスフィルタ」と「微分器(微分動作)」で構成されいている。
- インパルス信号\(e\)は、ローパスフィルタを通過することで急峻な変化が平滑化される。(突発的な一瞬の変化を小分けにしているようなイメージ)
- 微分した応答の波形こそ違うが、直接微分する(赤実線)よりも、平滑化したインパルス信号を微分する(青実線)ことで過大な微分動作を抑えつつ、緩やかな微分の機能が得られる。

図3:不完全微分の仕組み
このようにローパスフィルタの平滑化を備えた微分動作を不完全微分(Lagged derivative「遅れをもった微分」)という。
さて、不完全微分の機能を使いこなし、その性能を調整できるようになるためにも、ボード線図を使った周波数応答を見てみることにする。図4は、基本的な微分動作(青実線)、ローパスフィルタ(赤実線)、不完全微分(緑実線)におけるそれぞれのゲイン特性であり、\(T_d=8.0[s]\)、\(\mbox{η}=0.125\)で設定した。まず、図3のブロック線図の通り、不完全微分はローパスフィルタと微分器の伝達関数の縦続接続なので、そのゲイン特性はデシベル表記の場合、それぞれの和として表される。詳しく見ていくと、低い周波数帯域で微分の特性を残しつつ、高い周波数帯域では微分の特性をなくしている(=周波数に比例して増幅させないようにしている)ことがわかる。要するに、不要な信号を除去 or 緩和しつつ、微分の機能を働かさせる仕組みは、周波数別にその機能を分けているからであり、フィルタを取り付けることでこのような機能の合成を実現できるのである。
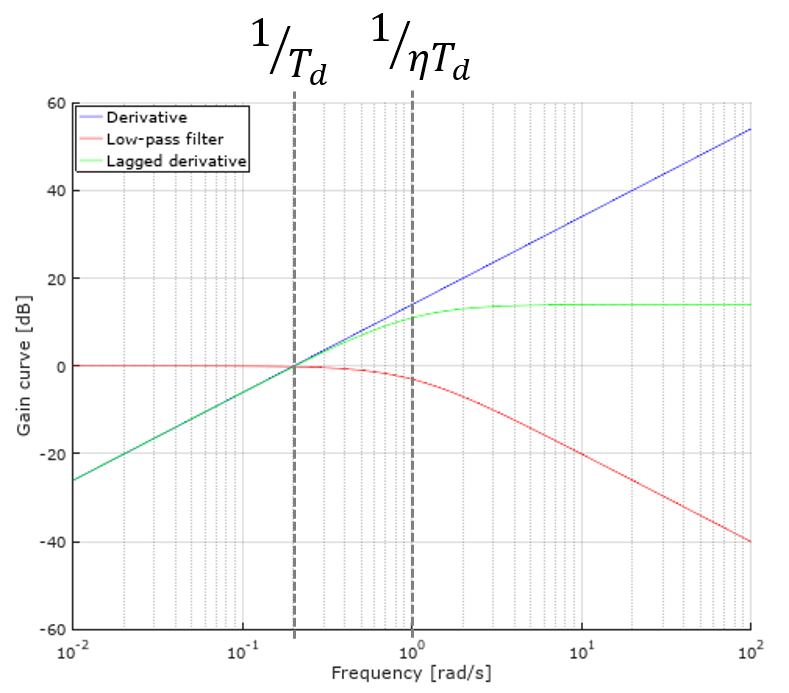
図4:ボード線図
調整のための性質を整理すると、
- ローパスフィルタのカットオフ周波数は\(\frac{1}{\mbox{η}T_d}\)で、微分時間\(T_d\)に連動して動く。\(\mbox{η}\)は0.1~0.125が推奨値?となっている。(\(T_d\)と\(\mbox{η}T_d\)の各定数の周波数上の位置関係は図4の通りである)
- \(T_d\)の調整は、ゲイン特性を左右に平行移動させる効果がある。つまり、
- ノイズを除去とは言うが、正しくは1(デカード)当たり-20(dB)のローパス特性(=一次遅れフィルタ)だと、それ以上は周波数に比例して増幅させない程度の機能しかない。
となる。ローパス特性が微分動作に依存している点は、現場などで具体的な調整が難しい際に役立つが、よりいい性能を求めるならば個別に設計することも十分に考えられる。
不完全微分の実装
続いて、実装のための過程を示す。スタートは図2のブロック線図の通り、以下の伝達関数のから始める。
\begin{align}U_D(s) &= \frac{T_ds}{1+\gamma T_ds}E(s) \label{eq:eq20180224-1} \end{align}
ただし、\(T_d\)は微分時間、\(\gamma\)は\(\eta\)の代わりで微分係数、\(U_D\)は微分動作の出力である。通常の微分方程式に戻した後、後進差分近似・式を整理することにより、以下の(\ref{eq:eq20180224-3})式が得られる。
\begin{align} u_D(k) + \gamma T_d\frac{u_D(k)-u_D(k - 1)}{T_s} &= T_d\frac{e(k)-e(k - 1)}{T_s} \notag \\ u_D(k) &= -f_1u_D(k - 1) +g_0\Delta e(k) \label{eq:eq20180224-3} \end{align}
ただし、\(\Delta e(k)=e(k)-e(k - 1)\)である。ここで、
\begin{align} f_1&=-(\frac{\gamma T_D}{T_s})/(1+\frac{\gamma T_d}{Ts}) \label{eq:eq20180224-4} \\ g_0&=(\frac{T_D}{T_s})/(1+\frac{\gamma T_d}{Ts}) \label{eq:eq20180224-5} \end{align}
と置いた。ここまでは、位置型PID制御としての計算過程なので、速度型PID制御にするために、
\begin{align} \Delta u_D(k)&= u_D(k) - u_D(k - 1) \label{eq:eq20180224-6} \end{align}
とする必要がある。よって、ソースコードは以下のとおりである。
% 不完全微分 f1 = -eta*Td/Ts/(1+eta*Td/Ts); g0 = Td/Ts/(1+eta*Td/Ts); ~ % ---------- PID制御シミュレーション ----------- for k = (1:N)+k_offset % プラントシミュレーションと制御量の計測 y(k) = -a1*y(k-1)+b0*u(k-td-1)+d(k)+a1*d(k-1); % 制御偏差の計算 e(k) = r(k)-y(k); % PID制御コントローラによる操作量の計算(PID制御則) ud(k) = -f1*ud(k-1)+g0*(e(k)-e(k-1)); du = kp*((e(k)-e(k-1))+Ts/Ti*e(k)+(ud(k)-ud(k-1))); u(k) = u(k-1)+du; end
ηの推奨値は、0.1~0.125だったりしますが、なぜその値かはよくしりません。あしからず。
不完全微分による効果
ここでは、図1の微分動作がよくない働きをする例を用いて、不完全微分の効果を確認する。注目してほしいのは、操作量の不必要な動作が緩和されている点、また、\(T_d=0\)にするよりも、不完全微分を使った方が過大な操作量を抑えつつも微分動作を発揮できている点である。
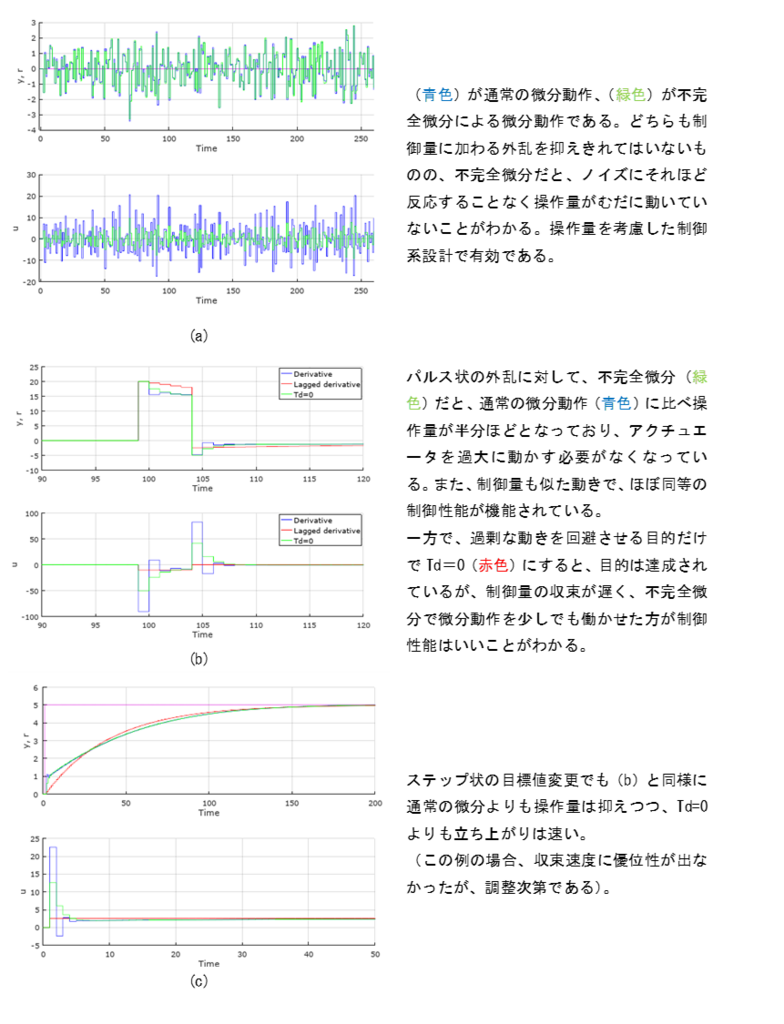
図4:不完全微分の例
まとめ
目標値応答にしても外乱応答にしても、その過渡応答を改善し目標値に速やかに収束させる微分動作は、より良い自動化のために必要なものです。今回、そんな微分動作の弱点を少しでも克服し、実践で使えるようにする不完全微分を紹介しましたが、有効性に気づいてもらったかと思います。それでも、実際のところは、不完全微分だけじゃ不十分だという事例はたくさんありますが、微分のもつ有効性に改めて気づかされる要素技術だと思います。
微分動作にまつわる経験として。現場に出たとき、そこに設定されている微分時間が0だったり、「微分時間のチューニングの仕方だけがよくわからない」と聞いたり、非常に悔しいと思うことがありました。制御関係で就職した(い)人だと、学校で学んだ制御工学と現場の制御工学が違うと感じる場面があるかと思います。制御を学んだことがある人として、少しでも役に立つ(理論的な)技術は普及していきたいものです。(ちなみに、不完全微分はほとんどデフォルトでDCSの機能に組み込まれ有効な状態だったりしますが、それでも外乱やノイズには悩まされます...)